量子系统在特定任务上可超越经典系统,这一概念被称为量子优势。尽管先前有各种集中于计算加速方面的量子优势研究(即量子计算优越性),但其优势会随着经典算法的进步而动态变化,经典系统无法达成的、具有可证明性的量子优势仍然难以实现。最新的研究实现了一种学习效率或信息获取效率上的量子优势,且任何经典机制在从原理上都无法到达,证实了量子策略从根本上超越经典策略的可行性。
最近,丹麦工业大学(DTU)的研究团队在光子平台上成功实现了量子学习优势[1]。要理解这一飞跃,必须先明白经典方法的根本瓶颈:海森堡不确定性原理。这个原理决定了任何测量本身都带有一层无法消除的“量子迷雾”——即固有的量子噪声。对于经典方法而言,要测量的微弱信号完全被这层浓雾所淹没。唯一的出路就是“蛮力统计”:进行天文数字般的重复测量,期望通过海量数据的平均来让信号从噪声中“浮现”出来。因此,随着系统复杂性的增加,所需测量的数量将呈指数级增长,为实际分析和校准造成了不可逾越的障碍。
这项研究的巧妙之处在于,它没有试图“消除”量子噪声,而是利用量子纠缠这条捷径直接绕过了它。研究人员利用EPR纠缠态和连续变量Bell测量,显著降低了对多模随机位移过程学习所需的采样复杂度,相比经典方法减少了11.8个数量级,并在120模实验中展示了9.2个数量级的可证明量子优势。这一突破性成果于9月25日发表在国际学术期刊《科学》(Science)上,标志着基于光子平台的大规模量子学习优势成为可能,为高维量子计量学和量子机器学习奠定了基础。

在研究量子系统特性时,常规策略受固有量子噪声的限制,样本复杂度随系统规模呈指数级增长,导致常规策略在某些学习任务中并不适用。为此,研究人员提出量子学习策略,利用量子相干性,通过集体量子测量方法显著降低了样本复杂度[2]。虽然此前有研究人员在40量子比特超导电子平台上演示了量子学习优势[3],但在更实际的场景中实现可扩展的量子学习优势还未能实现。
在本研究中,研究人员在可拓展的光子平台上,利用光学参量振荡器(OPO)操控量子涨落,产生特定压缩水平的两模压缩真空态(EPR纠缠态)。
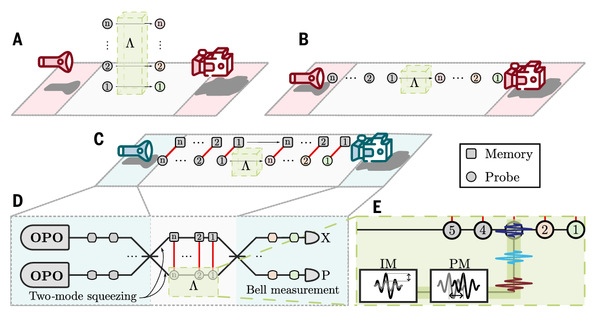
图1 A:常规多模学习策略 B:常规多时间学习策略 C:量子增强学习策略 D:压缩光的量子学习的实现 E:随机位移过程
处于纠缠状态的两路光束被不对称分配:一束充当与嘈杂系统相互作用的探针,而另一束则用作稳定的参考。他们通过利用一个非平衡分束器将弱相干态注入探针光束,对探针光束施加随机位移的方式来模拟系统的噪声。通过干涉探针光束和参考光束并进行零差探测来测量所得输出信号的振幅和相位正交分量,从而执行贝尔测量。OPO在贝尔测量期间实现了高达68%的噪声功率降低,从而能够高精度地检测位移过程的效应。
他们通过利用贝尔测量结果重建一类三峰位移过程的特征函数λ(β),展示了学习任务的量子增强。对于100模位移过程,最强压缩(-4.48dB)下的样本复杂度保持在约107,而通过指数拟合,无纠缠方案所需的样本复杂度高达7.3×1018,体现了11.8个数量级的进步。
《Science》期刊编辑Ian S. Osborne对此研究评价道:“这些结果表明,当前的光子技术可以实现大规模、可证明的量子优势,并且代表着量子计量和机器学习中实用的量子增强学习协议迈出了关键一步。”
这项工作表明量子纠缠可以从根本上加速信息获取,而且这些优势可以通过现实的、可扩展的光子技术来实现,有望将量子传感和机器学习推向新的高度。
参考资料
[1] Zheng-Hao Liu et al., Quantum learning advantage on a scalable photonic platform. Science 389, 1332-1335(2025).
[2] Huang H Y, Kueng R, Preskill J. Information-Theoretic Bounds on Quantum Advantage in Machine Learning[J]. Physical Review Letters, 2021, 126(19): 190505.
[3] Hsin-Yuan Huang et al. Quantum advantage in learning from experiments. Science 376, 1182-1186(2022).
