近期,哈佛大学与美国中性原子量子计算公司QuEra联合提出了一种“横向算法容错(Transversal Algorithmic Fault Tolerance)”的量子纠错新架构,可以将量子纠错的时间开销降低一个数量级以上。相关工作以“Low-Overhead Transversal Fault Tolerance for Universal Quantum Computation”为题发表在国际学术期刊《自然》(Nature)上[1]。

© Nature
背景介绍
量子计算依托量子态的叠加、纠缠等特性可以实现远超经典计算的算力。然而,由于量子态的脆弱性,人们不得不使用多个物理比特去编码一个逻辑比特,并在计算过程中不断测量、纠正已有错误,从而抵抗各种噪声的干扰。这一过程被称作量子纠错。
量子纠错虽然保证了可靠性,却带来了显著的时间与资源开销。例如,对于表面码(surface code)量子纠错码,使用传统纠错策略去破解2048位的RSA密钥,大概需要千万级别的物理比特稳定运行五到六天[2],这是一个极具挑战且开销极大的任务。
针对上述挑战,研究人员通过结合横向操作(transversal operations)与关联解码(correlated decoding)两项核心技术,提出了横向算法容错的架构,并使用表面码为例,从理论和数值模拟两方面证明了其优秀的容错性能。
横向操作
表面码是一种编码在二维物理比特阵列上的纠错码,假设阵列边长为d,则该纠错码可以至多容忍d个物理错误的发生,故又称d为码距。如果将两个表面码各自的物理比特一一执行量子门操作,可以直接实现两个表面码之间的等效的逻辑门操作。这种同时操作的方法就是横向操作。下图展示了一个在中性原子阵列上实现的横向纠缠门,可见横向操作直观、简洁,并行性高。
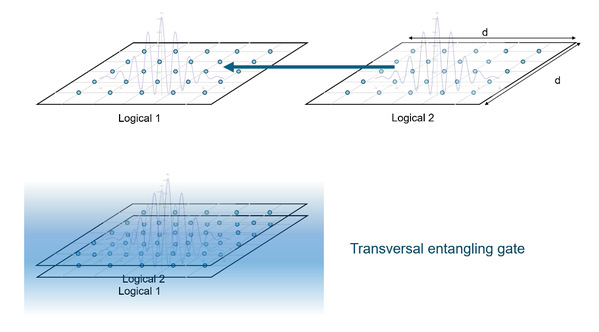
图1. 横向纠缠门操作示意图[3]
关联解码
传统的量子纠错方法要求每个子线路(如图2(a)红框部分)保证独立容错性,需要对错误进行逐个测量和解码(症状提取),例如表面码需要O(d)轮。而该研究工作新提出的关联解码不再要求子线路的准确,而是通过联合分析测量结果,仅仅确保整个线路的逻辑输出准确,这样所需的测量轮数就远小于d。这种创新的架构将纠错耗时从O(d)降低到了O(1)。
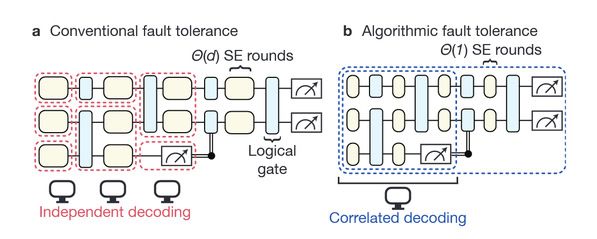
图2. (a) 传统解码方式需要d轮症状提取。(b) 综合解码方式只需要1轮症状提取
容错性论证和数值模拟
提出横向操作+关联解码的横向算法容错架构后,研究人员论证了该方法的容错性。具体来说,在关联解码中只得到了系统的部分信息,如果出现测量错误或纠错失误,就会导致在多轮测量中出现前后不一致的情况(如图3(c))。对此,注意到不论是编码操作还是横向门操作,其发生的错误在线路中的传播都是可以追溯的,因此可以通过外部的经典计算机可靠推断出逻辑测量结果,从而进行可靠的关联解码(如图3(d)),这样就可以实现横向门操作+综合解码的总体容错性。
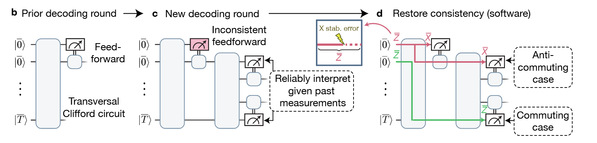
图3. 通过外部分析实现多轮纠错的前后一致性,进而实现容错运算
为了进一步证明该容错方案的有效性,研究人员以表面码为例,用含噪模型对该横向算法容错架构进行了数值模拟。如下图所示,该架构下表面码有明显的错误阈值,当物理比特错误率p<pth≈0.85%时,码距越大则逻辑错误率越低(如图4(a)),而横向算法逻辑错误率随码距呈指数下降(PL~exp(-Θ(d))(如图4(b)),证实了该架构是有效容错的。
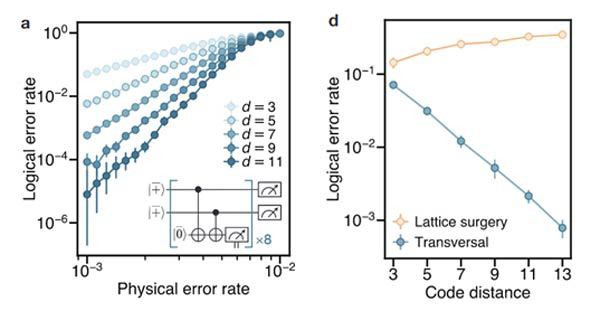
图4. 对横向容错算法做数值模拟。(a) 右方交叉处为阈值pth≈0.85% (b) 横向操作错误率随码距呈指数下降
总结
这项工作聚焦“量子纠错时空开销”这一根本难题,提出并证明了横向容错算法架构的可行性,将量子纠错的时空开销从O(d)降低到了O(1),这不仅向量子计算实用化迈出了重要一步,也展现了量子纠错算法还有巨大提升空间。
值得注意的是,中性原子量子计算体系的高可重构性[4,5]可以高效实现的横向操作。鉴于中性原子已经实现了数十个逻辑比特、数百个逻辑横向门以及纠错演示[6],该方案也为中性原子量子平台提供了清晰的未来实验路径。
参考文献
[1]. Zhou Hengyun et al., “Low-overhead transversal fault tolerance for universal quantum computation”, Nature (2025).
[2]. Zhou Hengyun et al. “Resource Analysis of Low-Overhead Transversal Architectures for Reconfigurable Atom Arrays”, Proceedings of the 52nd Annual International Symposium on Computer Architecture (2025).
[3]. Dolev Bluvstein, “Error-corrected quantum processing with neutral atoms”, Phd thesis, Harvard University, May 7, 2025.
[4]. Rui Lin et al., “AI-Enabled Parallel Assembly of Thousands of Defect-Free Neutral Atom Arrays”, Phys. Rev. Lett. 135, 060602 (2025).
[5]. Chiu Neng-Chun et al., “Continuous operation of a coherent 3,000-qubit system”, Nature (2025).
[6]. Bluvstein Dolev et al., “Logical quantum processor based on reconfigurable atom arrays”, Nature 626, 58 (2024).
